Picchettamento della curva con uso della sola cordella metrica e calcolo elementare dei dati di campagna.
Nell’articolo “OPERE PUBBLICHE SCADENTI PER INADEGUATEZZA DI TRACCIAMENTO” visibile in in questo sito è spiegato come molti manufatti di tipo nastriforme recentemente costruiti, ad esempio strade, canali, marciapiedi, aiuole, cordonate ecc, siano veramente brutti da vedersi perché realizzati senza un accurato tracciamento preventivo. E’ anche indicato come a far difetto siano sopratutto i raccordi al vertice dei rettifili i quali, invece di corrispondere ad altrettanti archi di circonferenza tangenti ai rettifili stessi, seguono dei percorsi casuali a raggio vario e anch’esso casuale perchè tracciati, come si usa dire, ad occhio, cioè senza applicare alcuna delle normali regole di tracciamento.
In questa breve nota si consiglia l’utilizzazione del cosiddetto “metodo del quarto” quale valida alternativa di quelli classici in quanto, pur non potendo sostituirli appieno, può evitare gran parte dei difetti di cui si è detto.
L’uso più semplice riguarda il tracciato di un arco di circonferenza definito da tre punti e cioè quello di inizio e di fine nonché del suo punto mediano. Si tratta quindi di materializzare nel terreno un arco circolare essendo note la corda e la freccia.
Il metodo usufruisce di una regola approssimativa in base alla quale, per archi di cerchio aventi angolo al centro di entità modesta, la freccia di una prima porzione pari alla metà dello sviluppo, corrisponde con molta approssimazione ad un quarto di quella dell’intero. Per tracciare tutta la curva è quindi sufficiente dividere a metà ed in successione ciascuno dei tratti già definiti innalzando dalla mezzeria della relativa corda una freccia di valore pari ad un quarto di quella precedente.
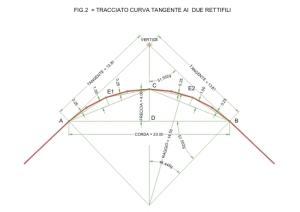
 Ad esempio con riferimento alla figura 1 nella quale risultano definiti e materializzati sul terreno i punti A, B, C di base si hanno i seguenti valori:
Ad esempio con riferimento alla figura 1 nella quale risultano definiti e materializzati sul terreno i punti A, B, C di base si hanno i seguenti valori:
Corda iniziale = A – B = 20.00 m Freccia iniziale = C – D = 4.00 m
Frecce successive (regola del quarto) rispettivamente 1.00 m, 0.25 m, 0.063 m, 0.016 m ecc.
Da rilevare come i valori esatti sarebbero: 1.037 m, 0.262 m, 0.066 m, 0.016, e quindi molto vicini a quelli calcolati empiricamente.
Il tracciato della curva ha luogo innalzando dalla mezzeria delle corde A-C e C-B una freccia lunga m. 1.00 con cui si ottengono i due nuovi punti E1 ed E2 della curva. Il raccordo, a questo punto, risulta diviso in quattro parti. Dalla mezzeria delle relative quattro corde si innalzeranno quattro frecce lunghe m. 0.25 definendo i punti F1, F2, F3, F4. La curva è ora definita da otto punti e otto corde dalla cui mezzeria si potranno innalzare altrettante frecce lunghe m. 0.063. La procedura può essere ripetuta a piacere fino a definire il tracciato con sufficiente dettaglio.
Qualora si volesse conoscere il valore del raggio di curvatura basterà applicare la seguente formula
Raggio=0.5 corda/(sen(2 x arccos(freccia/0.5corda))
NB. : ArcTang = angolo corrispondente alla tangente
Nell’esempio si ottengono i seguenti risultati:
Raggio = 10.00 m/sin(2 x arccos 0.400) =14.500 m
Il metodo è valido per archi di cerchio nei quali la freccia non sia superiore al 20% della corda il che corrisponde ad un angolo superiore o inferiore ad un angolo retto rispettivamente per quello al vertice e per quello al centro.
Nell’esempio la percentuale della freccia rispetto alla corda è pari esattamente al 20%. Si tratta quindi del limite estremo di applicabilità del metodo. Per le percentuali inferiori la precisione dei risultati sarà ancora migliore di quella, già buona, dell’esempio stesso.
Vediamo ora l’applicazione del metodo del quarto nella esecuzione del tracciato classico delle opere nastriformi che costituisce lo scopo precipuo da raggiungere: il raccordo circolare di due rettifili (vedi Figura 2)
La prima operazione da effettuare è la determinazione sul terreno del vertice operata prolungando i due rettifili fino al loro punto di intersezione C che è, appunto, il vertice. Si passa quindi alla
definizione dei punti di tangenza A e B cioè dei punti nei quali si desidera abbia inizio e fine il raccordo.
Essa avrà luogo, molto semplicemente, riportando lungo i due rettifili una stessa lunghezza, chiamata tangente, a partire dal vertice. Il valore della tangente rappresenta l’unica variabile in gioco dalla quale dipendono le caratteristiche dell’opera e cioè il suo percorso reale ed il suo raggio di curvatura. I due punti di tangenza quindi devono essere scelti con cura, se necessario sperimentando diverse varianti, in modo da verificare, a tracciato completato, quale sarà la reale ubicazione delle opere ed il loro impatto con i luoghi tenute presenti le due seguenti inderogabili condizioni idi base.
1° Le due tangenti devono essere equivalenti.
2° Il raggio di curvatura, una volta fissate le tangenti, è fisso ed invariabile per tutto lo sviluppo della curva.
E’ da rilevare come siano proprio queste due regole di base che nella realtà vengono sistematicamente infrante ricorrendo ad adattamenti empirici di tracciato al fine di adeguarlo alle caratteristiche reali del terreno: il risultato finale, come già detto, è pessimo.
Dirò di più. Molto spesso nei lavori di cui si parla non viene nemmeno determinato il vertice dei due rettifili!
Una volta definite accuratamente le tangenti, si misurerà la corda cioè la distanza A-B che intercorre tra i due punti di tangenza. A questo punto sarà possibile calcolare il valore della prima freccia inserendo i due elementi noti cioè corda e freccia nelle seguenti formule.
Alfa = metà angolo al centro= =ArcCos(mezza corda/tangente)
Freccia(1) = mezza corda x tan (Alfa/2)
Raggio= mezza corda/sen alfa
N.B.:
-ArcTang = angolo corrispondente alla tangente indicata
-Alfa = metà angolo al centro
Esempio:
Si abbia Tangente = 13.810 m e
Corda = 20.00 m
Si calcoleranno i seguenti elementi di tracciamento.
Alfa= mezzo angolo al centro = ArcCos(10.00 m/13.81 m)= ArcCos 0.724 = 48.448 gradi centesimali.
Freccia(1)= 10.00 m x tan 24.224 = 4.00 m
Raggio = 10.00m/sen48.448=14.50m
N.B.: L’angolo al centro è pari a 96,896 gradi centesimali e quindi inferiore ad un angolo retto, il metodo è quindi ammissibile.
Per il calcolo delle frecce degli elementi di tracciato successivo si userà la regola del quarto, come segue.
Freccia iniziale = 4.00 m
Frecce successive (regola del quarto) rispettivamente 1.00 m, 0.25 m, 0.063 m, 0.016 m ecc. . Per il picchettamento della restante parte della curva vale quanto detto per il precedente esempio.
L’unico limite di applicabilità del metodo descritto è dato dall’ampiezza dell’angolo al vertice che, come già precisato, deve essere superiore all’angolo retto pena la eccessiva approssimazione dei risultati.
E’ però da tener presente come in tutti i casi in cui la curva da tracciare ecceda tale limite, si può ricorrere ad un artificio estremamente semplice e cioè alla suddivisione della curva in due settori concentrici ognuno dei quali rientra entro i limiti imposti.
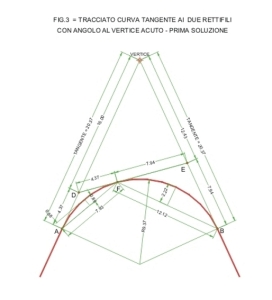
Facendo riferimento alla fig 3 relativa a due rettifili che si intersecano al vertice C con un angolo troppo piccolo che non consente l’uso diretto del metodo del quarto si traccerà l’allineamento D – E che determina, sui due rettifili originari i due sottovertici D E.
Il valore della tangente A – C sarà ottenuto con la:
A C = (DV + DE + EV)/2
Riportando tale lunghezza a partire dal vertice si picchetteranno i due punti di tangenza A e B mentre il nuovo punto di tangenza F comune alle due sottocurve sarà ottenuto riportando la distanza AD oppure BE lungo la DE.
A questo punto sono materializzati tutti gli elementi sufficienti per tracciare tutto lo sviluppo della curva applicando due volte la regola del quarto rispettivamente per la prima e la seconda porzione di curva. Ne risulterà un raccordo circolare a raggio unico e tangente ad ambedue i due rettifili originari.
Nell’esempio di fig 3 si svrà:
Tangente=(16.00+12.32+12.43)/2=20.37
Riportando sul terreno la tangente 20.37 si potranno misurare tangenti e corde come segue:
Prima semicurva, tang.=7.94, corda=12.12
Seconda semicurva, tangente =4.7, corda = 7.93
Si calcoleranno quindi le frecce:
Prima semcurva
Alfa=arccos(6.06/7.94)=44.753 gradi centesimali
Freccia=6.06*tang 22.367
Raggio=6.06/sen44.753=9.37
Seconda semicurva
Alfa=arccos(3.965/4.37)=27.803 gradi centesimali
Freccia=3.965*tang13.901=0.89
Raggio=3.965/sen27.803=9.37
Anche in questa operazione la posizione definitiva dell’opera è funzione del valore della tangente. In sede esecutiva sarà quindi opportuno sperimentare diverse soluzioni variando la posizione dell’allineamento DE da cui dipende il valore della tangente definitiva.
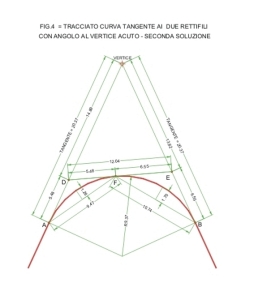
Per quanto riguarda la direzione angolare di detto allineamento C- D, fermo restando che essa è ininfluente ai fini della precisione del tracciato, è però consigliabile scegliere una direzione che, anche in via molto approssimativa sia perpendicolare alla bisettrice dell’angolo al vertice. In questo modo si otterranno delle corde della prima porzione di curva, simili a quelle della seconda il ché porterà ad una picchettazione abbastanza omogenea. Negli altri casi i punti tracciati apparterranno comunque all’arco di circonferenza ma ci sarà una notevole differenza fra le distanze della prima serie di punti da quelle della seconda serie. (vedi figura 4)
A conclusione di questa breve nota si può affermare che, anche nella presente era tecnologica, l’antico metodo del quarto può trovare un utile impiego nel tracciamento delle curve e dei raccordi circolari per la semplicità con cui permette di materializzare in loco un arco di cerchio a raggio unico, tangente ai rettifili e coincidente, con l’approssimazione di pochi centimetri, con quello condotto con il metodo rigoroso.
Si è anche dimostrato come il limite della metodologia dato dall’ampiezza dell’angolo al vertice dei due rettifili da raccordare possa facilmente essere superato suddividendo, se necessario, il tracciato in due parti.
Quelle descritte sono, in definitiva, operazioni topografiche semplici e più che sufficienti per una corretta costruzione delle comuni opere nastriformi come strade, canali, marciapiedi, cordonate, aiuole ecc. e che, per giunta, non richiedono che una attrezzatura assolutamente elementare: una cordella metrica, un metro da muratore ed una macchinetta calcolatrice che dia le funzioni trigonometriche degli angoli.
aggiornato marzo 2006
–
–